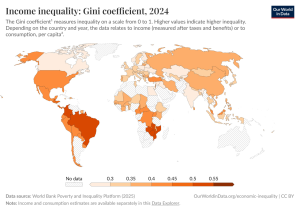
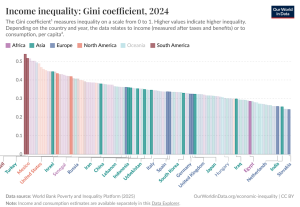
ضریب جینی یا شاخص جینی، رایج‌ترین معیار اندازه‌گیری نابرابری است. این شاخص توسط آمارشناس ایتالیایی کورادو جینی (1884-1965) توسعه داده شد و به نام او نامگذاری شده است. این شاخص معمولاً به عنوان معیاری برای نابرابری درآمدی استفاده می‌شود، اما می‌تواند برای اندازه‌گیری نابرابری هر توزیعی – مانند توزیع ثروت یا حتی امید به زندگی – نیز مورد استفاده قرار گیرد.

این شاخص نابرابری را در مقیاسی از 0 تا 1 اندازه‌گیری می‌کند، که در آن مقادیر بالاتر نشان‌دهنده نابرابری بیشتر است. این شاخص گاهی اوقات می‌تواند به صورت درصدی از 0 تا 100٪ نشان داده شود که «شاخص جینی» نامیده می‌شود. مقدار 0 نشان‌دهنده برابری کامل است: همه درآمد یکسانی دارند. مقدار 1 نشان‌دهنده نابرابری کامل است، جایی که یک نفر تمام درآمد را دریافت می‌کند و بقیه هیچ چیزی دریافت نمی‌کنند.

این شاخص در عین حال که نابرابری درآمدی را اندازه‌گیری می‌کند اما نابرابری‌های فرصت را نمی‌تواند اندازه‌گیری کند. از آن مهمتر این شاخص نابرابری‌های حاصل از ثروت نیز نمی‌تواند سنجش کند.

ضریب جینی چگونه محاسبه می‌شود؟

دو روش اصلی برای محاسبه ضریب جینی وجود دارد. هر دو به یک مقدار می‌رسند، اما دو زاویه مختلف برای درک آنچه که اندازه‌گیری می‌کند، در اختیار ما قرار می‌دهند.

روش ۱: ضریب جینی به ما می‌گوید که انتظار داریم بین درآمد هر دو نفر نسبت به میانگین، چه تفاوتی وجود داشته باشد.

روش اول را می‌توان با آزمایش فکری زیر نشان داد. تصور کنید دو نفر به طور تصادفی در خیابان با هم برخورد می‌کنند. آنها درآمد خود را مقایسه می‌کنند و متوجه می‌شوند که یک نفر در مقایسه با دیگری چقدر ثروتمند است. انتظار داریم چه شکافی وجود داشته باشد؟ این شکاف مورد انتظار بین دو نفر که به طور تصادفی انتخاب شده‌اند، همان چیزی است که ضریب جینی اندازه‌گیری می‌کند. این شکاف با در نظر گرفتن میانگین شکاف بین همه جفت افراد محاسبه می‌شود.

در جایی که درآمدها به طور مساوی توزیع شده‌اند، انتظار داریم شکاف بین دو نفر که به طور تصادفی انتخاب شده‌اند، کوچک باشد. در جایی که نابرابری زیاد است، انتظار داریم شکاف بزرگ باشد. با این حال، اگر به صورت مطلق اندازه‌گیری شود، این به میزان ثروتمند یا فقیر بودن کلی جمعیت نیز بستگی دارد. جایی که حتی مرفه‌ترین افراد جامعه درآمد پایینی دارند، شکاف مطلق بین درآمد افراد نمی‌تواند زیاد باشد. برعکس، جایی که درآمدها عموماً بالا هستند، حتی تفاوت‌های نسبی بسیار کوچک بین درآمد افراد می‌تواند منجر به شکاف‌های مطلق بزرگی شود.

به همین دلیل، ضریب جینی شکاف مطلق مورد انتظار بین درآمد افراد را نسبت به میانگین درآمد در جمعیت بیان می‌کند. به طور خاص، به عنوان شکاف مورد انتظار به عنوان سهمی از دو برابر میانگین درآمد محاسبه می‌شود. دو برابر میانگین درآمد، بالاترین مقدار ممکن برای شکاف متوسط ​​است – وضعیتی از نابرابری کامل، که در آن یک نفر تمام درآمد را دارد و بقیه هیچ درآمدی ندارند. بنابراین در این حالت از حداکثر نابرابری، ضریب جینی 1 است. کمترین مقدار ممکن برای شکاف متوسط ​​بین همه جفت‌های افراد صفر است – وضعیتی از برابری کامل، که در آن هیچ شکافی بین درآمد هیچ دو نفری وجود ندارد زیرا همه درآمد یکسانی دارند. در این حالت، ضریب جینی 0 است.

روش دوم: ضریب جینی به ما می‌گوید که «منحنی لورنز» چقدر از برابری کامل فاصله دارد.

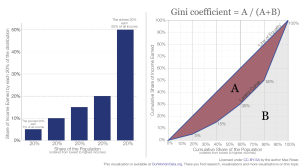
این شکل، تعریف بصری دوم از ضریب جینی را نشان می‌دهد. پنل سمت چپ، سهم درآمد دریافتی توسط هر پنجم از یک جمعیت فرضی را نشان می‌دهد. پنل سمت راست، این داده‌ها را به صورت تجمعی ترسیم می‌کند. این به عنوان «منحنی لورنز» شناخته می‌شود. در جمعیتی که درآمد کاملاً به طور مساوی تقسیم می‌شود، منحنی لورنز یک خط مورب مستقیم خواهد بود: 10٪ از جمعیت 10٪ از کل درآمد، 20٪ از افراد 20٪ از کل درآمد و غیره را کسب می‌کنند. این در نمودار به عنوان «خط برابری» نشان داده شده است.

با این حال، در جمعیت فرضی نشان داده شده است که در نمودار، درآمدها به طور مساوی توزیع نمی‌شوند. 60٪ از جمعیت در پایین‌ترین سطح درآمد، 30٪ از کل درآمد را کسب می‌کنند. ضریب جینی با مقایسه‌ی مساحت‌های A و B، میزان فاصله‌ی منحنی لورنز از «خط برابری» را نشان می‌دهد که به روش زیر محاسبه می‌شود:

ضریب جینی = A / (A + B)

منحنی لورنز «خط برابری» است که در آن درآمدها کاملاً به طور مساوی تقسیم می‌شوند. مساحت A برابر با 0 است و از این رو ضریب جینی نیز همینطور است. در جایی که یک نفر تمام درآمد را دارد و بقیه هیچ درآمدی دریافت نمی‌کنند، منحنی لورنز در امتداد محور پایین نمودار حرکت می‌کند – سهم تجمعی درآمد تا آخرین نفر صفر است. مساحت B برابر با صفر خواهد بود و ضریب جینی برابر با 1 خواهد بود.

انتقادات علمی وارد بر ضریب جینی

ضریب جینی شاخصی ساده و پراستفاده برای سنجش تمرکز یا پراکندگی درآمد است، اما این سادگی با محدودیت‌های روش‌شناختی و تفسیری همراه است. پژوهش‌های نظری و تجربی متعدد نشان داده‌اند که ضریب جینی در شرایط مشخصی می‌تواند گمراه‌کننده باشد یا اطلاعات مهم توزیع را پنهان کند. سادگی، قابلیت مقایسه بین کشورها و شهرت بین‌المللی، باعث شده است تا ضریب جینی در بسیاری از گزارش‌های اقتصادی و اجتماعی استفاده شود. اما در کنار مزایا، این شاخص محدودیت‌ها و ایرادهایی نیز دارد که شناخت آن‌ها برای تحلیل درست نابرابری ضروری است (Atkinson, 1970; Cowell, 2000). در ادامه به برخی از نواقص و ایرادهای علمی این شاخص اشاره می‌شود:

1. از دست رفتن جزئیات توزیع درآمد

یکی از اصلی‌ترین نقدها بر ضریب جینی آن است که این شاخص تنها «یک عدد» از کل توزیع ارائه می‌دهد و نمی‌گوید نابرابری در کجای جامعه رخ داده است. بنابراین ضریب جینی یک مقدار عددی تک‌بعدی است و بنابراین اطلاعات مربوط به شکل توزیع (مانند سهم‌دهی انتهای بالا در برابر پایین یا تغییرات میانه) را از بین می‌برد. دو توزیع با ساختارهای کاملاً متفاوت (مثلاً «فشار در طبقه میانی» در یکی و «افزایش سهم طبقه بالا» در دیگری) می‌توانند همان ضریب جینی را داشته باشندAtkinson, 1970; Cowell, 2000) ).

به عنوان مثال ممکن است دو کشور ضریب جینی برابر 0/35 داشته باشند، اما در یکی طبقه‌ متوسط کوچک بوده و ثروت در دست عده‌ای بسیار محدود متمرکز باشد؛ در حالی‌که در دیگری، اختلاف فقط بین طبقات بالا و پایین است. با وجود این تفاوت، ضریب جینی هر دو کشور یکسان است. در نتیجه، ضریب جینی نمی‌تواند نشان دهنده این باشد که آیا نابرابری ناشی از فقر گسترده است یا ناشی از تمرکز ثروت در قشر بالا است. به زبان ساده، ضریب جینی فقط وجود نابرابری را نشان می‌دهد، اما نمی‌تواند معین کند که «کجای جامعه و به چه شکلی» این نابرابری شکل گرفته است و همچنین جامعه از چه توزیع درآمد و ثروتی برخوردار است.

2. سوگیری در نمونه‌های کوچک و خطای برآورد (Small-Sample Bias)

تحقیقات تجربی نشان داده‌اند که برآورد کلاسیک ضریب جینی در نمونه‌های کوچک دارای سوگیری است و معمولاً مقدار واقعی نابرابری را پایین‌تر یا گاهاً نادرست نشان می‌دهد. دلتاس نشان می‌دهد که در نمونه‌های کوچک (یا در تحلیل زیرنمونه‌های کوچک) ضریب جینی به‌طور سیستماتیک اشتباه برآورد می‌شود.(Deltas, 2003) به عنوان نمونه ضریب جینی در داده‌هایی که تعداد نمونه کم است (مثلاً بررسی چند منطقه یا چند گروه خاص) ممکن است دقیق نباشد. از این رو در این حالت، شاخص ضریب جینی معمولاً کمتر از مقدار واقعی برآورد می‌شود، یعنی نابرابری واقعی بیشتر از چیزی است که شاخص نشان می‌دهد. این خطا به «سوگیری نمونه کوچک» معروف است و باعث می‌شود پژوهش‌هایی که در مقیاس‌های خرد (مثلاً سطح شهرستان یا روستا) انجام می‌شوند، نیازمند روش‌های اصلاحی باشند.

3. حساسیت (یا عدم حساسیت) به انتهای توزیع و مسئله «دم‌سنگین» (fat tails)

شاخص ضریب جینی به نسبتِ تغییرات در میانه توزیع حساس‌تر است و ممکن است تغییرات در «دمِ بالایی» (یعنی ثروتمندان بسیار کم‌شمار ولی بسیار ثروتمند) یا دمِ پایینی را به‌درستی نشان ندهد. مطالعاتی همچون کاول (2002) به حساسیت شاخص‌ها به مقادیر بسیار بزرگ Outliers) ) پرداخته‌اند و طالب (2015) به‌صورت ویژه استدلال می‌کند که برای توزیع‌هایی با دنباله‌های ضخیم fat tails)) روش‌های محاسبه معمول ضریب جینی بسیار ناپایدار و گمراه‌کننده‌ است و روش‌هایی مبتنی بر برآورد پارامترهای دنبالهtail exponent) ) را توصیه می‌کند (Cowell, 2002; Taleb, 2015).

ضریب جینی بیشتر به تغییرات در بخش میانی جامعه (طبقه‌ی متوسط) حساس است و تغییرات شدید در دو سر توزیع — یعنی فقیرترین یا ثروتمندترین افراد — را به خوبی نشان نمی‌دهد  .(Cowell & Flachaire, 2002)به عنوان مثال، اگر در کشوری گروه کوچکی از میلیاردرها بسیار ثروتمندتر شوند، ممکن است ضریب جینی تغییر چندانی نکند، در حالی‌که نابرابری واقعی افزایش یافته است.

4. مشکلات تجزیه‌پذیری و تفکیک منابع درآمد (Decomposition)

درآمد مردم از منابع مختلفی مانند حقوق، سود سرمایه، یارانه یا اجاره و امثال آن حاصل می‌شود. برای تحلیل نقش منابع مختلف درآمد (مانند درآمد، دستمزد، سرمایه، انتقالی) باید بتوان شاخص کلی را به سهم مؤلفه‌ها تجزیه کرد. اما ضریب جینی به‌راحتی قابل «تجزیه» بر اساس منبع درآمد نیست. روش‌های مختلف تجزیه برای ضریب جینی مانند روش‌های Shorrocks، Lerman–Yitzhaki یا Dagum وجود دارند، اما هر یک محدودیت‌ها و فروض خاص خود را دارند. به‌ویژه زمانی که درآمدهای منفی یا همبستگی بین منابع وجود داشته باشد، تفسیر نتایج دشوار و حتی گمراه‌کننده می‌شود و ممکن است نتایج نادرست بدهند(Lerman & Yitzhaki, 1985; Dagum, 1997) . بنابراین در واقع، ضریب جینی نمی‌تواند توضیح دهد که کدام بخش از اقتصاد یا کدام نوع درآمد عامل نابرابری است.

5. مسائل داده‌ای و تفاوت‌های آماری میان کشورها

یکی دیگر از محدودیت‌های مهم شاخص ضریب جینی، مربوط به مقایسه این نرخ میان کشورهاست. زیرا در کشورهای مختلف، «درآمد» ممکن است به‌صورت‌های گوناگون تعریف شود. در برخی از کشورها درآمد قبل از مالیات و برخی پس از مالیات محاسبه می‌شود و همچنین برخی کشورها درآمد خانوار را می‌سنجند و برخی درآمد فردی را ملاک و معیار قرار می‌دهند. علاوه بر این در بسیاری از کشورها بخش بزرگی از درآمد غیررسمی در آمار رسمی دیده نمی‌شود. به همین دلیل، مقایسه‌ی مستقیم ضریب جینی بین کشورها ممکن است تصویر نادرستی ارائه دهد Cobham & Sumner, 2013)). برای نمونه ممکن است کشوری با ضریب جینی پایین‌تر در ظاهر برابرتر باشد، در حالی‌که فقط بخش قابل‌ مشاهده‌ درآمد در آمار آمده است و اقتصاد غیررسمی نادیده گرفته شده است.

از این رو مقایسه ضریب جینی بین کشورها با مشکلاتی از قبیل تفاوت در تعریف «درآمد» (پیش/پس از مالیات، درآمد خانواده یا فردی، درآمد قابل‌تصرف یا ناخالص)، تفاوت در پوششِ داده‌ها (برآورد نشدن اقتصاد غیررسمی یا درآمدهای سرمایه‌ای بالا)، و روش گردآوری (مصاحبه، اظهارنامه مالیاتی، نمونه‌گیری) همراه است و هر یک از این موارد می‌توانند باعث تفاوت‌های ساختگی در ضریب گزارش‌شده شوند. بنابراین بدون توجه به همگنی داده‌ها، مقایسه‌ها قابل‌اطمینان نیستند (Cowell, 2000; Cobham & Sumner, 2013).

6. محدود بودن به بُعد مالی نابرابری

ضریب جینی تنها توزیع درآمد یا ثروت را می‌سنجد و سایر ابعاد نابرابری مانند دسترسی به آموزش، بهداشت، فرصت‌های شغلی و امنیت اجتماعی را در بر نمی‌گیرد. به گفته‌ «آمارتیا سن» نابرابری فقط به پول مربوط نیست، بلکه به «توانایی واقعی افراد برای داشتن زندگی مطلوب» نیز وابسته است  .(Sen, 1997)به همین دلیل شاخص‌های چندبعدی رفاه(Multidimensional Indices Walfare)  یا شاخص‌های ترکیبی مانند شاخص توسعه انسانی(HDI)  یا شاخص «پالما» (Palma Ratio) می‌توانند تصویر جامع‌تری از نابرابری اجتماعی ارائه دهند (Cobham & Sumner, 2013).

بر این اساس این شاخص صرفاً توزیعِ یک کمیت (معمولاً درآمد یا مصرف) را می‌سنجد و جنبه‌های دیگری از نابرابریِ اجتماعی مانند دسترسی به سلامت، آموزش، فرصت‌های اجتماعی یا جابجایی بین نسلی را مورد ارزیابی قرار نمی‌دهد. از این رو برای تحلیل پیامدهای اجتماعی و رفاهی، استفاده از شاخص‌های تک‌بعدی کافی نیست و چارچوب‌های چندبعدی ضرورت دارد (Sen, 1997 ; Atkinson, 1970)

7. تأثیر ساختار خانوار و جمعیت

تغییرات جمعیتی و خانوادگی می‌توانند ضریب جینی را تغییر دهند، حتی بدون اینکه تغییری در توزیع واقعی درآمد رخ دهد. برای مثال، اگر خانواده‌ها کوچک‌تر شوند یا افراد ثروتمند مهاجرت کنند، ضریب جینی ممکن است افزایش یا کاهش یابد، در حالی‌که قدرت خرید یا سطح واقعی زندگی در جامعه ثابت مانده است (Cowell, 2000). بنابراین هنگام تحلیل نابرابری، باید تغییرات جمعیتی را نیز در نظر گرفت تا تفسیر شاخص دقیق‌تر شود. بر این اساس تغییر در اندازه و ترکیب خانوار (مثلاً کاهش اندازه خانوار، مهاجرتِ انتخابیِ نیروی کار) می‌تواند ضریب جینی را تحت تأثیر قرار دهد، بدون آنکه تغییری واقعی در نابرابریِ درآمدی فردی رخ داده باشد.

با توجه به این محدودیت‌ها، اقتصاددانان پیشنهاد می‌کنند که ضریب جینی نباید به‌تنهایی ملاک ارزیابی نابرابری باشد. برای درک دقیق‌تر، استفاده‌ هم‌زمان از شاخص‌های مکمل مانند شاخص اتکینسون Atkinson Index))، شاخص‌های آنتروپی تعمیم‌یافته (Generalized Entropy) ) و نسبت درآمد بین دهک‌های بالا و پایینPalma Ratio) ) توصیه می‌شود (Atkinson, 1970; Cowell, 2000; Cobham & Sumner, 2013).) همچنین برای داده‌های کوچک یا دارای توزیع نامتعارف، باید روش‌های اصلاح آماری و برآورد دقیق‌تر به‌کار رود (Deltas, 2003; Taleb, 2015).).

نتیجه‌گیری

ضریب جینی یکی از ابزارهای مشهور برای اندازه‌گیری نابرابری است، اما یک معیار ناقص و اولیه است و نباید آن را معیار مطلق دانست. این شاخص تنها در بیان شدت کلی نابرابری یک عدد تعیین می‌کند، اما از توضیح ساختار، علت‌ها و جهت تغییرات نابرابری و سایر ابعاد نابرابری ناتوان است. بنابراین در مطالعات اقتصادی و اجتماعی، تکیه‌ صرف بر ضریب جینی می‌تواند تصویر ناقص و حتی گمراه‌کننده‌ای از وضعیت واقعی جامعه ارائه دهد. ترکیب این شاخص با ابزارهای تکمیلی و تحلیل‌های چندبعدی، راهی علمی‌تر برای درک و مقابله با نابرابری است.

از این رو به دلیل محدودیت‌های فوق برای پژوهشگران و سیاست‌گذاران و علاقمندان راهکارهای زیر برای سنجش نابرابری توصیه می‌شود:

✅ استفاده همزمان از چند شاخص از جمله شاخص ضریب جینی، شاخص اتکینسون، شاخص‌های آنتروپی تعمیم‌یافته «Generalized Entropy» و شاخص‌های نسبت‌های بین دهکی مانندPalma) ) برای سنجش دقیق و ذوابعاد نابرابری و ارائه تصویر کامل‌تری از توزیع درآمد.

✅ اعمال اصلاح‌های نمونه‌ای و برازش توزیع برای کاهش سوگیری در نمونه‌های کوچک یا توزیع‌های دم‌سنگین (Deltas, 2003; Taleb .(2015

✅ انجام تجزیه‌پذیری دقیق با روش‌های مناسب و گزارش فروض مورد استفاده Lerman & Yitzhaki, 1985; Dagum, 1997)).

✅ ترکیب اندازه‌گیری درآمد/مصرف با شاخص‌های چندبعدیِ رفاه و فرصت .(Sen, 1997)

منابع

Atkinson, A. B. (1970). On the measurement of inequality. Journal of Economic Theory, 2(3), 244–263. https://www.sciencedirect.com/science/article/abs/pii/0022053170900396

Cobham, A., & Sumner, A. (2013). Is it all about the tails? The Palma measure of income inequality (CGD Working Paper No. 343). Centre for Global Development. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2366974

Cowell, F. A. (2000). Measuring inequality (2nd ed.). Oxford University Press. https://www.researchgate.net/publication/227468229_Measuring_Inequality

Cowell, F., & Flachaire, E. (2002). Sensitivity of inequality measures to extreme values. London School of Economics. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1094842

Deltas, G. (2003). The small-sample bias of the Gini coefficient: Results and implications for empirical research. Review of Economics and Statistics, 85(1), 226–234. https://www.jstor.org/stable/3211637

Dagum, C. (1997). A new approach to the decomposition of the Gini income inequality ratio. Empirical Economics, 22(4), 515–531. https://link.springer.com/article/10.1007/BF01205777

Lerman, R. I., & Yitzhaki, S. (1985). Income inequality effects by income source: A new approach and applications to the United States. Review of Economics and Statistics, 67(1), 151–156. https://www.jstor.org/stable/1928447

Sen, A. (1997). On economic inequality (2nd ed.). Oxford University Press. https://sen.scholars.harvard.edu/publications/economic-inequality

Taleb, N. N. (2015). How to (not) estimate Gini coefficients for fat-tailed variables. arXiv preprint arXiv:1510.04841.

https://ourworldindata.org/what-is-the-gini-coefficient

https://ourworldindata.org/grapher/economic-inequality-gini-index?tab=map